In the world of AI-generated text, controlling randomness is essential. Two primary techniques—Top-K and Top-P (nucleus) sampling—determine how language models like GPT-4 or Claude decide what word comes next when generating text.

Whether you’re building AI products, fine-tuning prompts, or simply curious about how AI works, understanding these two concepts will help you balance creativity and predictability in your AI-generated content.

🔍 What is Top-K Sampling?

Top-K sampling restricts the model to select the next token from only the K most probable options. From this limited set, one token is randomly chosen based on their relative probabilities.

🧠 Analogy:

Imagine choosing a dish at a restaurant, but only considering the top 5 chef’s recommendations. You’ll pick randomly among those 5—reliable options with some variety.

• K = 1 → Greedy decoding; always selects the single most likely next token (deterministic)
• K = 40 → Conservative, mostly predictable outputs
• K = 100 → More variety while maintaining relevance
• K = 500+ → Much broader selection, potentially less focused

🎯 What is Top-P Sampling?

Top-P sampling (nucleus sampling) takes a dynamic approach. Instead of a fixed number, it selects the smallest possible set of tokens whose cumulative probability reaches or exceeds P (e.g., 0.9 or 90%). It then samples randomly from this dynamic set.

🧠 Analogy:

Rather than limiting yourself to a fixed number of menu items, you consider all dishes that collectively make up 90% of all orders. This might be 3 popular dishes on a simple menu or 15 items on a diverse one—the selection adapts to the context.

• P = 0.5 → High creativity, less predictable
• P = 0.8-0.9 → Balanced approach (most common)
• P = 0.95 → More conservative, higher accuracy
• P = 1.0 → No filtering (equivalent to sampling from full vocabulary)

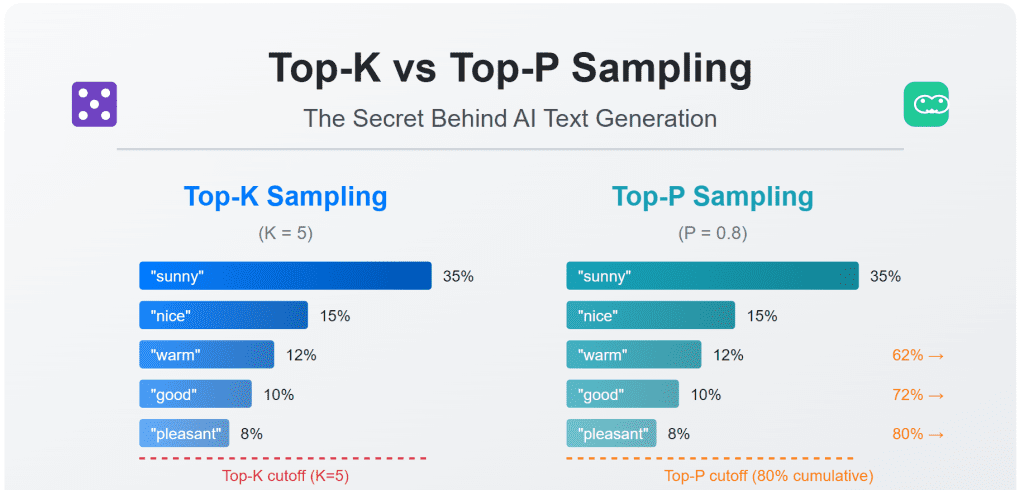
📊 Visualization: How They Work

Probability distribution for next token after "The weather is":

Token      | Probability
-----------+------------
" sunny"   | 0.35
" nice"    | 0.15
" warm"    | 0.12
" good"    | 0.10
" pleasant"| 0.08
" hot"     | 0.07
" beautiful"| 0.05
" perfect" | 0.03
" great"   | 0.02
... others | 0.03 (combined)

Top-K (K=3) would only consider: " sunny", " nice", and " warm" (total prob: 0.62)

Top-P (P=0.7) would consider: " sunny", " nice", " warm", and " good" (total prob: 0.72)

🎬 Simulation Example: Prompt = "What is 1 + 2?"

Let’s examine how these sampling methods behave with a simple math prompt:

✅ Top-K = 1 (Greedy Decoding)

The model always selects the #1 most probable token at each step.

Input: "What is 1 + 2?"
Model prediction (showing top 5 candidates):
- " The" (0.45)
- " It's" (0.20)
- " Answer:" (0.12)
- " 1" (0.08)
- " In" (0.05)

Selected: " The" (highest probability)
Context: "What is 1 + 2? The"

Next prediction:
- " answer" (0.62)
- " result" (0.15)
- " sum" (0.10)
- " total" (0.05)
- " value" (0.03)

Selected: " answer"
Context: "What is 1 + 2? The answer"

[Continuing process...]
Final output: "What is 1 + 2? The answer is 3."

Result: Precise, consistent, but potentially rigid or formal.

🎨 Top-P = 0.8 (Nucleus Sampling)

The model selects from tokens whose cumulative probability ≥ 0.8, then samples randomly based on their relative weights.

Input: "What is 1 + 2?"
Model ranks tokens (showing top candidates):
- " The" (0.45)
- " It's" (0.20)
- " Answer:" (0.12)
- " 1" (0.08)
- " In" (0.05)

Top-P (0.8) selection pool: " The", " It's", " Answer:", " 1" (total: 0.85)
Randomly selected: " It's" (based on relative probability)
Context: "What is 1 + 2? It's"

Next prediction pool includes:
- " 3" (0.35)
- " equal" (0.25)
- " obviously" (0.15)
- " simple" (0.10)

[Continuing process...]
Possible output: "What is 1 + 2? It's equal to 3!"
Alternative output: "What is 1 + 2? It's obviously 3."

Result: More natural variation in phrasing and expression, but maintains accuracy.

🌡️ The Temperature Factor

While Top-K and Top-P control the candidate pool, temperature influences how randomly the model samples from that pool:

• Temperature = 0.3-0.5: Conservative, focused on highest probabilities
• Temperature = 0.7-0.8: Balanced creativity and coherence
• Temperature = 1.0: Default setting, follows the model’s original probability distribution
• Temperature = 1.5-2.0: Increased randomness and creativity

Many systems use a combination of these parameters, such as temperature=0.7, top_p=0.9, top_k=50.

💻 Practical Implementation

Here’s how you might implement these sampling methods in Python with a language model:

# Pseudocode for sampling methods
def sample_next_token(logits, temperature=1.0, top_k=None, top_p=None):
    # Apply temperature
    logits = logits / temperature
    
    # Convert to probabilities
    probs = softmax(logits)
    
    # Apply Top-K filtering
    if top_k is not None:
        # Zero out all values not in top k
        values, indices = top_k_values_and_indices(probs, k=top_k)
        probs = zeros_like(probs)
        probs[indices] = values
        # Renormalize
        probs = probs / sum(probs)
    
    # Apply Top-P filtering
    if top_p is not None:
        # Sort probabilities
        sorted_probs, sorted_indices = sort_descending(probs)
        # Get cumulative probabilities
        cumulative_probs = cumulative_sum(sorted_probs)
        # Find cutoff index where cumulative prob >= top_p
        cutoff_idx = find_first(cumulative_probs >= top_p)
        # Zero out all values beyond cutoff
        probs_to_keep = sorted_indices[:cutoff_idx+1]
        probs = zeros_like(probs)
        probs[probs_to_keep] = sorted_probs[:cutoff_idx+1]
        # Renormalize
        probs = probs / sum(probs)
    
    # Sample from the filtered distribution
    next_token = random_choice(range(len(probs)), p=probs)
    return next_token

⚖️ When to Use Which Method?

Use Case	Top-K	Top-P	Temperature
Factual Q&A	K=10-40	P=0.9	T=0.3-0.7
Creative Writing	K=100+	P=0.7-0.9	T=0.7-1.2
Code Generation	K=10-40	P=0.95	T=0.2-0.5
Summarization	K=50	P=0.9	T=0.5-0.7
Brainstorming	K=100+	P=0.7	T=1.0-1.5

🚀 Best Practices

1. Use both methods together for optimal control (e.g., top_k=50, top_p=0.9)
2. Start conservative and increase parameters gradually
3. Consider context length: Longer contexts may need stricter parameters to stay on track
4. Different models respond differently: Parameters that work for GPT-4 may not be optimal for other models
5. Task-specific tuning: Creative tasks benefit from higher values, factual tasks from lower values

🎓 Advanced Perspective

Recent research suggests that sampling strategies significantly impact model hallucinations. More conservative sampling (lower temperature, higher Top-P values) tends to reduce factual errors but may increase model overconfidence.

The ideal sampling strategy isn’t universal—it depends on your specific use case, desired output style, and tolerance for creative vs. accurate responses.

---

Want more AI generation tips and technical deep dives? Subscribe for weekly insights on maximizing your AI tools!

---

Additional resources:

• Hugging Face documentation on sampling strategies
• OpenAI’s guide to completion parameters
• Paper: The Curious Case of Neural Text Degeneration (Holtzman et al.)